CALCULO INTEGRAL

Definición:

El cálculo integral es una rama de las matemáticas que se ocupa de la integración de funciones, es decir, de la búsqueda de áreas bajo curvas y volúmenes en el espacio tridimensional. La integración es una técnica fundamental para la resolución de problemas en muy diversas áreas, como la física, la ingeniería, la economía, entre otras.

Origen:

El cálculo integral tiene sus raíces en la antigua Grecia, donde los matemáticos como Arquímedes y Eudoxo desarrollaron técnicas para encontrar áreas bajo curvas y volúmenes de sólidos. Sin embargo, fue en el siglo XVII cuando los matemáticos como John Wallis y Isaac Barrow dieron un importante paso adelante al introducir el concepto de integral definida.

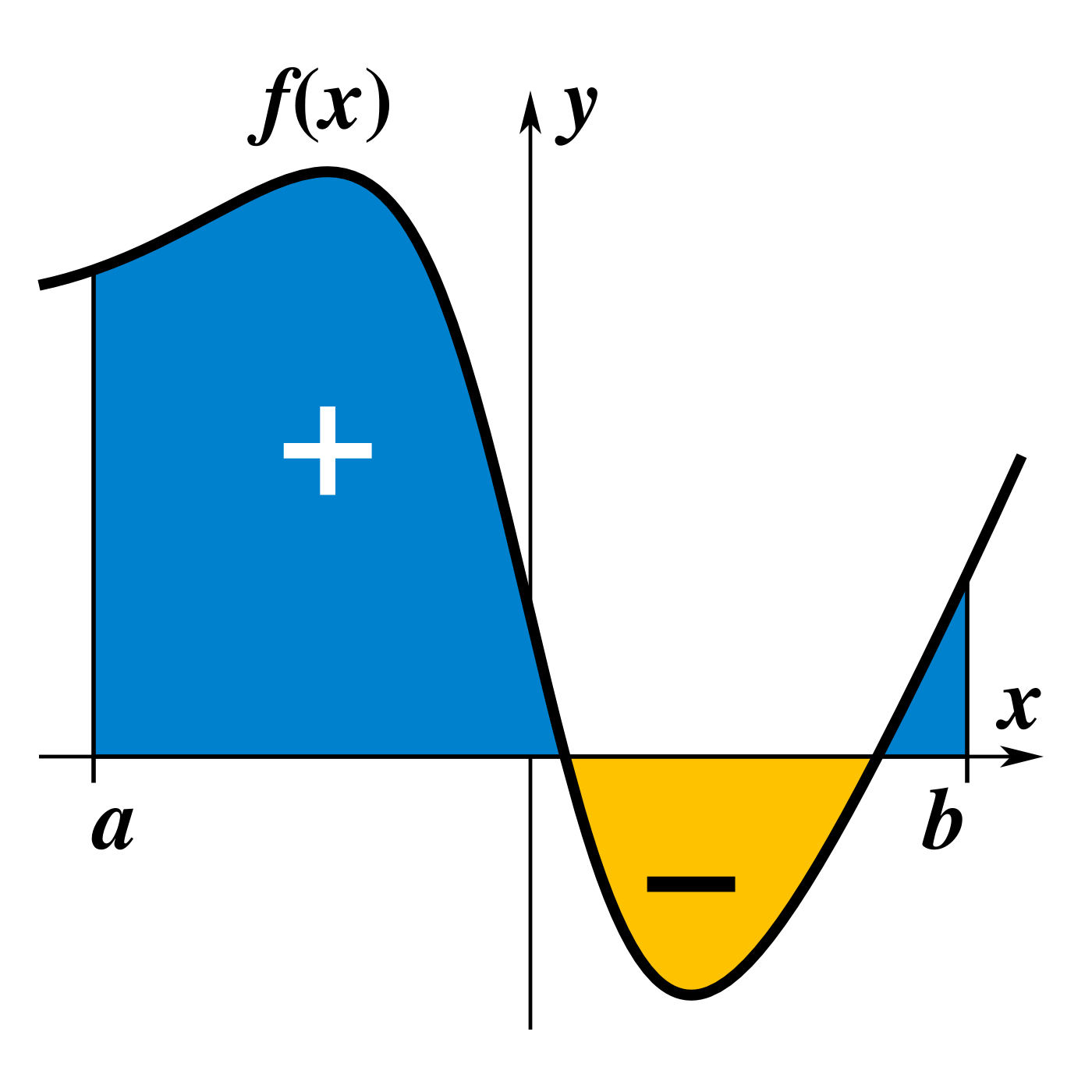
La integral definida es un concepto clave en el cálculo integral. Es una forma de medir el área bajo una curva o el volumen de un sólido en el espacio. La integral definida se representa matemáticamente como una función, que se calcula mediante la aplicación de una regla o fórmula específica.

Técnicas más utilizadas:

Una de las técnicas más utilizadas para calcular integrales definidas es la llamada regla de integración por partes. Esta técnica se aplica cuando se tienen integrales que incluyen funciones producto de dos funciones. La regla de integración por partes permite reemplazar la función producto por una combinación de funciones que pueden ser más fáciles de integrar.

Otra técnica importante en el cálculo integral es la llamada regla de integración por sustitución. Esta técnica se aplica cuando se tienen integrales que incluyen funciones que pueden ser expresadas en términos de otras funciones. La regla de integración por sustitución permite simplificar la función original, haciéndola más fácil de integrar.

Además de las reglas de integración por partes y por sustitución, existen muchas otras técnicas y fórmulas que se utilizan en el cálculo integral. Algunos de los conceptos más importantes incluyen las integrales impropias, las integrales dobles y triples, y las integrales en coordenadas polares.